Supervised Dimension Reduction
in Hydejack
이번 포스팅에서는 지도 차원 축소 방법 중 Forward Selection, Backward Elimination, Stepwise Selection, 그리고 Genetic Algorithm에 대해 살펴보겠습니다. 해당 포스팅은 고려대학교 산업경영공학과 강필성 교수님의 강의를 참고했음을 밝힙니다.
차원 축소
차원 축소는 왜 해야 할까요?
저희가 일반적으로 접하는 데이터들은 대부분 고차원의 데이터입니다. 고차원의 데이터는 모델의 성능을 저하시키는 노이즈를 가지고 있을 확률이 높고, 모델을 학습하는데 있어 높은 계산 복잡도를 가집니다. 또한, 모델의 일반화를 위해 많은 개수의 데이터를 필요로 한다는 문제점도 존재합니다. 이러한 고차원 데이터의 문제점을 해결하기 위해 도입된 해결 방안 중 하나가 바로 차원 축소입니다.
차원 축소는 여러 개의 변수가 존재하는 변수 집합에서 모델을 가장 잘 학습시킬 수 있는 변수의 부분집합을 찾거나 새로운 변수의 집합을 추출하는 것입니다. 이러한 차원 축소는 크게 지도 방법과 비지도 방법으로 나누어집니다. 먼저, 지도 차원 축소(supervesed dimension reduction)은 모델로부터 평가받은 차원 축소의 결과를 반영해 반복적으로 차원 축소를 진행함으로써 최종적으로 모델에 가장 적합한 변수의 부분집합을 찾는 방법입니다.
아래 그림의 Learning Algorithm에서 Supervised Feature Selection으로 이어지는 화살표가 바로 모델의 피드백을 반영해 다시 차원 축소를 진행하는 것을 나타냅니다. 따라서 지도 차원 축소는 모델의 평가를 기반으로 차원 축소를 진행하므로 동일한 데이터일지라도 모델에 따라 각각 다른 차원 축소 결과를 도출합니다.
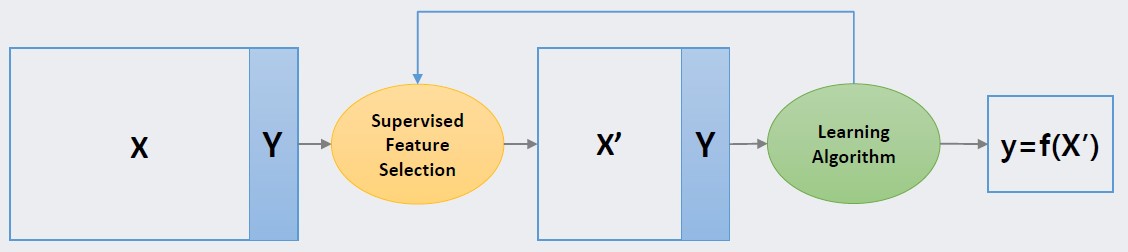Supervised Feature Selection
반면 비지도 차원 축소(unsupervesed dimension reduction)는 모델의 피드백 없이 분산, 거리 등과 같이 데이터로부터 추출할 수 있는 성질을 보존하는 저차원의 좌표계를 찾는 과정을 통해 새로운 변수의 집합을 추출하는 방법입니다. 따라서 지도 차원 축소와 다르게 데이터의 성질만을 바탕으로 차원 축소가 진행되므로 동일한 데이터에 대해 동일한 차원 축소 결과를 도출합니다.
Unsupervised Feature Selection
지금부터는 위에서 소개한 지도 차원 축소 방법 중 Forward Selection, Backward Elimination, Stepwise Selection, 그리고 Genetic Algorithm에 대해 차례대로 살펴보겠습니다. 앞의 4가지 지도 차원 축소 방법은 고차원의 데이터에서 변수를 선택함으로써 데이터의 차원을 축소하는 변수 선택법에 해당함을 먼저 알려드립니다.
Forward Selection (전진 선택법)
1. 전진 선택법
전진 선택법은 이름처럼 변수를 선택해 나가는 방법으로 변수가 없는 모델에서부터 시작해 유의미한 변수를 하나씩 추가하는 과정을 통해 변수를 선택합니다. 예를 들어, 아래 그림처럼 p개의 변수가 존재할 때, 가장 먼저 하나의 변수를 선택하는 과정을 거칩니다. 이 과정에서 선택되는 변수는 하나의 단일 변수로 모델을 학습시키거나 적합했을 때 가장 좋은 결과를 보여야겠죠? 그러므로 p개의 변수 각각에 대해 하나의 변수만을 이용한 p개 모델의 결과를 얻은 후, 그 중 가장 좋은 결과를 도출한 변수가 유의미한 변수라면 그 변수를 최종적으로 선택합니다. 그림에서는 3번째 변수가 선택되었습니다.
다음으로 이전 단계에서 선택된 변수는 고정시키고 해당 변수를 제외한 p-1개의 변수를 하나씩 추가해보며 위와 같은 과정을 거쳐 변수를 선택합니다. 즉, 총 두개의 변수로 학습한 p-1개의 결과 중 가장 좋은 결과를 보인 변수가 유의미하면 그 변수를 추가적으로 선택합니다. 그림에서는 5번째 변수가 두번째로 선택되었습니다.
위와 같은 과정을 반복해 선택되지 않은 변수들 중 가장 좋은 결과를 보이는 유의미한 변수를 추가적으로 선택함으로써 차원을 축소하는 방법이 바로 전진 선택법입니다.
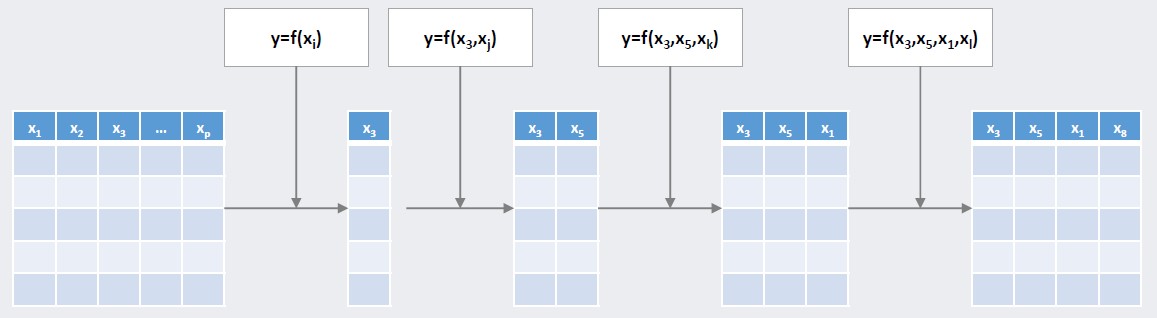Foward Selection
이론적으로는 위와 같은 과정을 모든 변수가 선택되는 마지막 단계까지 진행할 수 있으므로 총 p번의 반복수행이 가능합니다. 하지만 변수 선택 과정에서 유의미한 변수를 선택해야 하므로 선택되지 않은 변수들 중 가장 좋은 결과를 보이는 변수가 유의미하지 않다면 해당 단계에서 전진 선택법이 종료됩니다.
전진 선택법은 앞에서 설명한 것처럼 이전 단계까지 선택된 변수는 고정시키고 해당 변수들을 제외한 다른 변수들을 하나씩 추가해보고 비교하는 과정을 통해 변수를 선택하는 방법입니다. 따라서 한 번 선택된 변수는 절대 제거될 수 없다는 한계점을 가집니다.
2. 전진 선택법 구현
지금부터는 전진 선택법의 구현을 통해 알고리즘을 더 자세히 알아보겠습니다. 해당 구현에서는 여러 모델 중 회귀 모델을 기반으로 전진선택법을 진행했음을 알려드립니다.
먼저, 전진 선택법의 구현에 앞서 변수 선택과 변수의 유의미성 판단의 기준이 될 통계량에 대해 알아보도록 하겠습니다. 해당 코드는 회귀 모델을 기반으로 구현되었으므로 일반적으로 회귀 분석에서 주로 사용되는 아래와 같은 성능 지표를 이용하겠습니다.
- 변수 선택 지표: Akaike Information Criteria (AIC), 수정 결정계수
- 변수의 유의미성 판단 지표: p-value
먼저, 변수 선택의 기준이 되는 AIC는 종속 변수의 실제 분포와 모델에 지정된 분포 사이의 불일치에 대한 Kullback-Leibler 정보 측도를 기반으로 모델의 적합성과 복잡성을 반영하는 정보 지수입니다. AIC는 잔차제곱항 SSE에 변수의 개수 k에 대한 penalty term을 추가한 지표로 아래와 같이 계산되며, 아래 식의 왼쪽 항은 모델의 적합도를 의미해 작을수록 좋은 부분이고, 오른쪽 항은 모델의 복잡도를 나타내는 부분으로 작을수록 좋습니다. 따라서 AIC 값이 작을수록 더 좋은 모델이라고 볼 수 있습니다.
AIC=n\cdot \ln { \left( \frac { SSE }{ n } \right) } +2k다음으로 수정 결정계수는 회귀 모델의 적합도를 나타내는 지표인 수정계수를 기반으로 모델의 복잡도를 추가적으로 고려한 지표입니다. 기존의 종속변수의 전체 변동 SST 중 회귀식에 의해 설명되는 변동 SSR(=SST-SSE)의 비율인 결정계수에 변수의 개수 k에 대한 penalty term을 추가한 지표로 아래와 같이 계산되며, AIC와 반대로 값이 클수록 좋은 회귀 모델이라고 볼 수 있습니다.
{ R }_{ adj }^{ 2 }=1-\frac { n-1 }{ n-k-1 } \frac { SSE }{ SST }변수 선택의 지표인 AIC와 수정 결정계수의 계산식을 구현하면 아래와 같습니다.
SSE = np.sum((self.y - y_pred) ** 2)
SST = np.sum((self.y - np.mean(self.y)) ** 2)
AIC = self.n * np.log(SSE / self.n) + 2 * len(used_vars)
adj_R_sq = 1 - (self.n - 1) / (self.n - len(used_vars) - 1) * SSE / SST
위에서 소개한 두 변수 선택 기준에 이어 회귀 모델에서 변수의 유의미성을 판단하는 기준이 되는 p-value에 대해 살펴보겠습니다. p-value란 가설 검정에서 귀무가설을 지지하는 확률을 나타내는 지표입니다. 따라서, p-value가 작을수록 귀무가설(변수의 계수=0)을 지지하는 확률이 낮으므로 변수가 유의미하다고 볼 수 있습니다. 아래 그림에서 p-value는 빨간색 부분에 해당하며, 이를 구현한 코드는 다음과 같습니다.
p-value
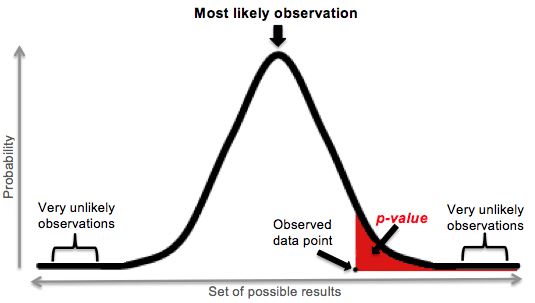
MSE = (sum((self.y - y_pred) ** 2)) / (len(const_X) - len(const_X.columns))
var_b = MSE * (np.linalg.inv(np.dot(const_X.T, const_X)).diagonal())
sd_b = np.sqrt(var_b)
ts_b = params / sd_b
pvalue = [2 * (1 - stats.t.cdf(np.abs(i), (len(const_X) - 1))) for i in ts_b]
위에서 소개한 세가지 평가 지표를 이용해 전진 선택법을 구현하겠습니다. 전진 선택법은 크게 선택되지 않은 변수들 중 추가되었을 때 가장 좋은 성능을 보이는 변수를 선택하는 과정과 선택된 변수의 유의미성을 판단하고 해당 변수가 유의미하면 최종적으로 선택하는 과정으로 나누어집니다.
먼저, 첫번째 과정은 설명변수 X, 종속변수 y, 현재까지 선택된 변수의 리스트 selected_vars, 그리고 변수 선택의 기준 eval_metric을 바탕으로 현재 단계에서 추가되었을 때 가장 모델의 성능이 좋은 변수를 선택하는 과정입니다. candidate_vars에 속하는 각 변수와 selected_vars를 이용해 기준값을 도출한 후 가장 좋은 성능을 보이는 변수를 찾습니다. 아래 구현에서는 기준이 AIC의 경우 낮을수록 좋은 모델이므로 AIC가 최솟값인 변수를, 수정 결정계수의 경우 높을수록 좋은 모델이므로 최댓값인 변수를 선택합니다.
candidate_vars = list(set(self.all_vars) - set(selected_vars))
candidate_vars_crt, pvalues = [], []
for i in range(len(candidate_vars)):
used_vars = selected_vars + [candidate_vars[i]]
candidate_var_crt, fitted_model = self.metric(used_vars)
candidate_vars_crt.append(candidate_var_crt[self.eval_metric])
pvalue = self.p_value(fitted_model, used_vars)
pvalues.append(pvalue)
if self.eval_metric == 'AIC':
selected_idx = np.argmin(candidate_vars_crt)
elif self.eval_metric == 'adj_R_sq':
selected_idx = np.argmax(candidate_vars_crt)
selected_var = candidate_vars[selected_idx]
selected_pvalue = pvalues[selected_idx][-1]
다음으로 두번째 과정은 현재까지 선택된 변수의 리스트 selected_vars, 위의 첫번째 과정을 구현한 함수 forward_cell, 변수의 유의미성 판단 지표인 p-value의 유의수준 alpha를 바탕으로 첫번째 과정에서 선택된 변수를 최종적으로 선택할 지 판단합니다. 첫번째 과정에서 1차적으로 선택된 변수의 p-value값인 selected_pvalue를 기준으로 그 값이 유의수준보다 작아 선택된 변수가 유의하면 최종적으로 선택하고, 유의하지 않으면 변수 선택을 종료합니다.
selected_var, selected_pvalue = self.forward_cell(selected_vars)
if selected_pvalue <= alpha:
selected_vars.append(selected_var)
else:
break
Backward Elimination (후진 소거법)
1. 후진 소거법
전진 선택법에 이어 지도 차원 축소에 속하는 후진 소거법은 전진 선택법과 반대로 변수를 제거하며 데이터의 차원을 축소하는 방법입니다. 예를 들어, 아래 그림처럼 6개의 변수가 존재할 때, 가장 먼저 모든 변수를 이용해 모델을 구축합니다. 그 후, 전체 변수 중 하나의 변수를 제거합니다. 이 과정에서 제거되는 변수는 해당 변수를 제외한 나머지 변수들로 모델을 학습시키거나 적합했을 때 가장 좋은 결과를 보여야겠죠? 그러므로 하나의 변수를 제거할 때, 6개의 변수 각각에 대해 하나의 변수를 제외한 5개의 변수를 통해 각각 구축한 총 6개의 모델 결과를 도출한 후, 그 중 가장 좋은 결과를 보이는 모델에 사용된 변수 집합을 도출합니다. 해당 변수 집합에 속하지 않은 변수가 유의미하지 않으면 해당 변수를 최종적으로 제거하게 됩니다. 즉, 총 5개의 변수로 학습한 6개의 결과 중 가장 좋은 결과를 보인 변수 집합에 속하지 않은 변수가 유의미하지 않다면 그 변수를 제거합니다. 아래 그림에서는 2번째 변수가 제거됐습니다.
다음으로 이전 단계에서 제거된 변수를 제외한 나머지 변수를 대상으로 앞의 과정을 통해 추가적으로 하나의 변수를 제거합니다. 그림에서는 4번째 변수가 두번째로 제거되었습니다. 위와 같은 과정을 반복해 제거되지 않은 변수들 중 제거됐을 때 가장 좋은 결과를 보이는 유의미하지 않은 변수를 추가적으로 제거함으로써 차원을 축소하는 방법이 바로 후진 소거법입니다.
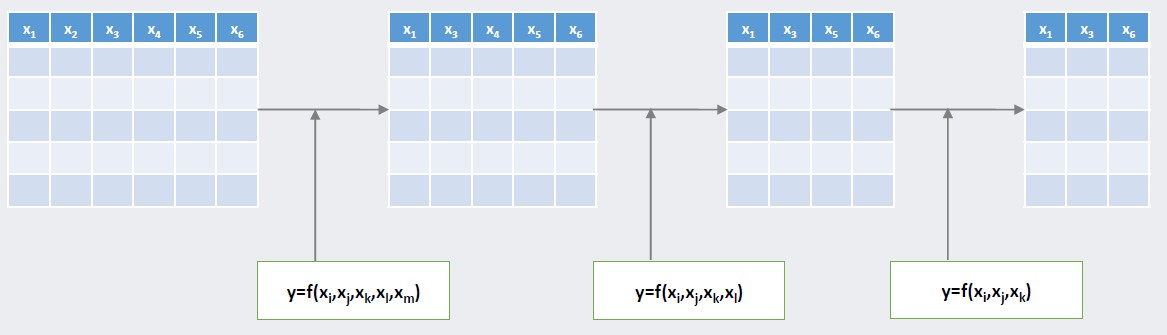Backward Elimination
이론적으로는 위와 같은 과정을 모든 변수가 제거되는 마지막 단계까지 총 p번의 수행할 수 있습니다. 하지만 변수 제거 과정에서 유의미하지 않은 변수를 제거해야 하므로 제거되지 않은 변수들 중 제거했을 때 가장 좋은 결과를 보이는 변수가 유의미하다면 해당 단계에서 후진 소거법이 종료됩니다.
후진 소거법은 앞에서 소개한 것처럼 제거했을 때 가장 좋은 결과를 보이는 유의미하지 않은 변수를 순차적으로 제거해 나가는 변수 선택법입니다. 따라서 한 번 제거된 변수는 다시 추가될 수 없다는 한계점을 가집니다.
2. 후진 소거법 구현
지금부터는 후진 소거법의 구현을 통해 알고리즘에 대해 더 자세히 알아보겠습니다. 해당 구현에서는 전진 선택법과 마찬가지로 여러 모델 중 회귀 모델을 기반으로 후진 소거법을 진행했음을 알려드립니다. 또한, 후진 소거법은 전진 선택법과 유사하므로 전진 선택법의 구현과 달라진 부분을 중점적으로 보도록 하겠습니다.
앞서 소개한 변수 선택 및 변수의 유의미성 기준인 AIC, 수정 결정계수 그리고 p-value를 기반으로 후진 소거법을 구현하겠습니다. 후진 소거법은 크게 제거되지 않은 변수들 중 제거되었을 때 가장 좋은 성능을 보이는 변수를 도출하는 과정과 도출된 변수의 유의미성을 판단하고 해당 변수가 유의미하지 않으면 최종적으로 해당 변수를 제거하는 두가지 과정으로 나누어집니다.
먼저, 첫번째 과정은 설명변수 X, 종속변수 y, 현재까지 선택된 변수의 리스트 selected_vars, 그리고 변수 선택의 기준 eval_metric을 바탕으로 현재 단계에서 제거되었을 때 가장 모델의 성능이 좋은 변수를 도출하는 과정입니다. 전진 선택법과 다르게 후진 소거법의 candidate_vars는 현재까지 선택된 변수입니다. 해당 candidate_vars에 속하는 각 변수를 제거한 나머지 변수 집합을 이용해 기준값을 도출한 후 제거했을 때 가장 좋은 성능을 보이는 변수를 찾습니다. 이후 전진 선택법과 동일한 변수 선택 기준 및 기준치를 통해 최종적으로 변수의 제거를 결정합니다.
used_X = np.take(self.X, selected_vars, axis=1)
fitted_model = self.model.fit(used_X, self.y)
pvalues = self.p_value(fitted_model, selected_vars)
candidate_vars = selected_vars
candidate_vars_crt = []
for i in range(len(candidate_vars)):
used_vars = candidate_vars[:i] + candidate_vars[i + 1:]
candidate_var_crt, fitted_model = self.metric(used_vars)
candidate_vars_crt.append(candidate_var_crt[self.eval_metric])
if self.eval_metric == 'AIC':
eliminated_idx = np.argmin(candidate_vars_crt)
elif self.eval_metric == 'adj_R_sq':
eliminated_idx = np.argmax(candidate_vars_crt)
eliminated_var = candidate_vars[eliminated_idx]
eliminated_pvalue = pvalues[selected_vars.index(eliminated_var)]
다음으로 후진 소거법의 두번째 과정은 현재까지 선택된 변수의 리스트 selected_vars, 위의 첫번째 과정을 구현한 함수 backward_cell, 변수의 유의미성 판단 지표인 p-value의 유의수준 alpha를 바탕으로 첫번째 과정에서 도출된 변수를 최종적으로 제거할 지 판단합니다. 해당 과정에서는 전진 선택법과 반대로 첫번째 과정에서 1차적으로 도출된 변수의 p-value값인 eliminated_pvalue 값이 유의수준보다 커 해당 변수가 유의미하지 않다면 최종적으로 제거하고, 유의하면 변수 제거를 종료합니다.
eliminated_var, eliminated_pvalue = self.backward_cell(selected_vars)
if eliminated_pvalue >= alpha:
selected_vars.remove(eliminated_var)
else:
break
Stepwise Selection (단계적 선택법)
1. 단계적 선택법
앞서 소개한 전진 선택법과 후진 소거법의 한계점을 보완하기 위해 제안된 단계적 선택법은 전진 선택법과 후진 소거법의 순차적인 반복을 통해 변수를 선택하는 방법이다. 단계적 선택법은 모든 변수를 포함하지 않는 모델을 시작으로 전진 선택법을 통해 가장 영향력이 크고 유의미한 변수를 추가합니다. 이후 전진 선택법과 후진 소거법을 순차적으로 반복해 변수를 추가하고 제거하는 과정을 통해 최종적으로 변수를 선택함으로써 차원을 축소합니다. 앞의 변수의 추가와 제거를 진행하는 과정에서 기존에 선택되거나 제거된 변수도 다시 선택과 제거의 대상이 되므로 이를 통해 위의 2가지 변수 선택법의 한계점을 보완한 것을 알 수 있습니다.
아래 그림처럼 p개의 변수가 존재할 때, 가장 먼저 전진 선택법을 통해 3번째 변수를 선택합니다. 이후 전진 선택법과 후진 소거법을 순차적으로 시행해 5번째 변수를 선택하고 3번째 변수를 제거합니다. 3번째 변수가 제거되는 과정에서 이전에 선택된 변수를 제거할 수 없는 한계점을 보완한 것을 확인할 수 있습니다. 이후 앞의 과정을 반복해 변수 선택을 진행하고 이전에 선택된 변수 집합이 변수 선택 이후에도 동일하다면 변수 선택과정을 멈추는 과정을 통해 차원을 축소하는 방법이 단계적 선택법입니다.
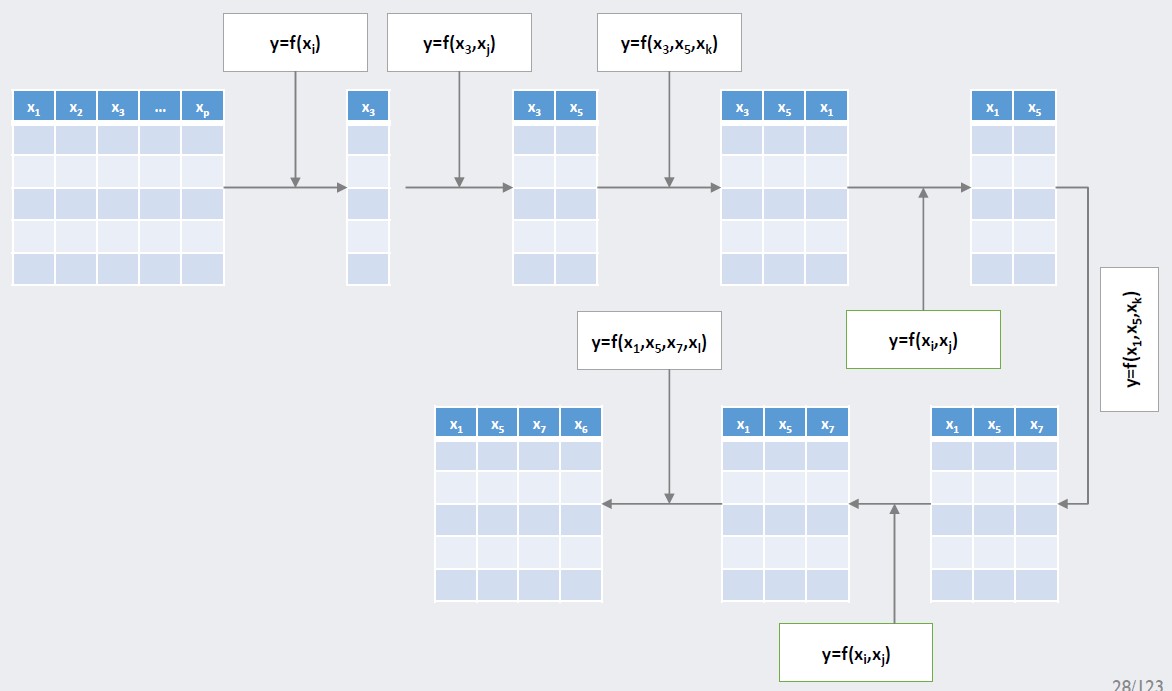Stepwise Selection
2. 단계적 선택법 구현
지금부터는 단계적 선택법의 구현을 통해 알고리즘에 대해 더 자세히 알아보겠습니다. 앞서 소개한 변수 선택법과 동일하게 회귀 모델을 기반으로 단계적 선택법을 진행했음을 알려드립니다. 또한, 앞에서 소개한 것처럼 단계적 선택법은 전진 선택법과 후진 소거법의 반복을 통해 구현되므로 위에서 구현한 forward_cell 함수와 backward_cell 함수를 사용하겠습니다.
전진 선택법과 후진 소거법의 순차적인 시행을 통해 진행되는 단계적 선택법은 전진 선택법의 경우 forward_cell 함수를 통해 도출한 selected_var의 p-value가 유의하면 변수를 최종적으로 선택합니다. 또한, 이어 진행하는 후진 소거법의 경우 backward_cell 함수를 통해 도출된 eliminated_var의 p-value가 유의하지 않으면 최종적으로 제거하는 과정을 반복합니다. 앞의 두 과정은 변수 선택 전후의 결과가 동일할 때까지 반복적으로 진행됩니다.
# do forward selection
selected_var, selected_pvalue = self.forward_cell(selected_vars)
if selected_pvalue <= alpha:
selected_vars.append(selected_var)
# do backward selection
eliminated_var, eliminated_pvalue = self.backward_cell(selected_vars)
if eliminated_pvalue >= alpha:
selected_vars.remove(eliminated_var)
## Stopping criteria
if before_selected_vars == selected_vars:
break
Genetic Algorithm (유전 알고리즘)
앞서 소개한 3가지 지도 차원 축소 방법은 변수의 모든 부분집합을 대상으로 최적해를 탐색하는 exhaustive search와 달리 일부의 부분집합만을 대상으로 탐색을 진행하는 local search에 해당합니다. Local search는 효율적인 탐색 방법이지만, search space가 제한적이기 때문에 최적해를 찾을 확률이 낮다는 한계점을 가집니다. 따라서 기존의 local search에 조금의 계산 과정을 추가해 위의 한계점을 보완함으로써 local search의 성능을 향상시킨 방법이 바로 유전 알고리즘입니다.
유전 알고리즘은 생물체가 환경에 적응하면서 진화해가는 모습을 모방하여 최적해를 찾아가는 방법입니다. 따라서 유전 알고리즘은 생물체에서 사용하는 용어를 차용하며, 그 개념은 아래와 같습니다.
- 염색체(chromosome): 생물학적으로 염색체는 유전 물질을 담고 있는 하나의 집합을 의미하며, 유전 알고리즘에서는 변수 선택을 나타내기 위한 표현으로 사용됩니다.
- 유전자(gene): 유전자는 염색체를 구성하는 요소로 하나의 유전 정보를 나타냅니다. 유전 알고리즘에서는 염색체에 존재하는 각 변수의 변수 선택 여부 encoding 정보 (선택=1, 미선택=0)이 유전자에 해당합니다.
- 자손(child chromosome): 유전 알고리즘에서 자손은 2개의 부모 염색체로부터 생성된 염색체를 의미하며, 부모 염색체를 일부를 섞는 crossover 과정을 통해 생성된 염색체입니다.
- 적합도(fitness): 적합도는 각 염색체가 가지고 있는 고유 값으로 어떤 염색체가 더 적합한지를 판단하는 기준이 됩니다. 예를 들어 회귀 분석의 경우 AIC, 수정 결정계수와 같은 값이 적합도에 해당합니다.
지금부터는 위에서 소개한 개념들을 바탕으로 유전 알고리즘의 과정에 대해 설명하겠습니다. 유전 알고리즘은 총 6단계로 아래와 같이 진행되며, 각 단계에 대해 자세히 살펴보겠습니다.
Genetic Algorithm Step
Step1: 염색체 초기화 및 파라메터 설정
유전 알고리즘은 변수 선택의 정보를 나타내는 염색체를 기반으로 진행됩니다. 따라서 유전 알고리즘을 시작하기에 앞서 변수 선택 정보를 표현하는 염색체를 초기화 해야하며, 해당 초기화 염색체들은 다양한 변수 선택 조합을 나타냅니다. 염색체의 길이는 변수의 개수와 동일하고 각 변수가 선택되면 1, 선택되지 않으면 0으로 표시하는 binary encoding을 통해 아래 그림과 같이 표현되며, 초기화 과정을 구현하면 다음과 같습니다.
Chromosome
chrom = np.random.choice([0, 1], size=(self.var_num), p=[1-self.chrom_ratio, self.chrom_ratio])
다음으로 염색체 초기화와 더불어 첫단계에서 유전 알고리즘의 파라메터를 설정합니다. 유전 알고리즘의 파라메터는 다음과 같습니다.
- the number of chromosome (population): 변수 선택의 조합을 나타내는 염색체의 개수로 해당 개수만큼의 염색체로 이루어진 population이 변수 선택의 후보가 됩니다. 아래 구현에서는 pop_size에 해당합니다.
- fitness function: 적합도를 계산하기 위한 지표로 회귀분석의 경우 AIC, 수정 결정계수와 같은 지표를 사용합니다. 아래 구현에서는 eval_metric에 해당합니다.
- crossober mechanism: 유전 알고리즘의 step5에 해당하는 crossover 과정에서 필요한 crossover point와 같은 파라메터를 의미합니다. 아래 구현에서는 crossover_point에 해당합니다.
- the rate of mutation: 유전 알고리즘의 step5에 해당하는 mutation 과정에서 필요한 mutation ratio를 나타냅니다. 아래 구현에서는 mutate_ratio에 해당합니다.
- stoppint criteria: 유전 알고리즘의 종료 조건을 의미하는 파라메터로 minimum fitness improvement, maximum iterations 등을 사용합니다. 아래 구현에서는 max_iter에 해당합니다.
Step2&3: 각 염색체 선택 변수 별 모델 학습 & 각 염색체의 적합도 평가 (Fitness Evaluation)
Step2&3에서는 이전 단계에서 초기화된 각 염색체에 대해 유전자 정보가 1인 변수들로 모델을 학습하고 해당 모델의 적합도를 평가하는 과정을 통해 population의 모든 염색체의 적합도를 산출합니다. population에 속하는 각 염색체에 대해 평가 지표 함수 eval_metric를 이용해 fitness를 산출하는 과정은 아래와 같이 구현됩니다. 해당 구현은 앞에서 소개한 3가지 변수 선택법과 마찬가지로 회귀 모델을 기반으로 하므로 metric 함수는 앞에서 소개한 metric 함수와 동일합니다.
selected_vars = [c for c, v in zip(range(self.var_num), chrom) if v == 1]
fitness = self.metric(selected_vars)[self.eval_metric]
Step4: 우수염색체 선택 (Selection)
Step4에서는 이전 단계에서 도출한 모든 염색체의 fitness 값을 기준으로 우수 염색체를 선택합니다. 우수 염색체를 선택하는 방법에는 크게 deterministic selection과 probabilistic selection이 있습니다. Deterministic selection은 fitness 값이 높은 상위 n개의 염색체를 선택하는 방법이고, probabilistic selection은 fitness에 대한 확률 값을 기반으로 n개의 염색체를 샘플링하는 방법입니다. 해당 구현에서는 probabilistic selection을 이용했으며, 아래와 같이 구현됩니다.
probs = fitness_values / sum(fitness_values)
top_n = int(self.pop_size * self.top_ratio)
selected_idx = np.random.choice(len(population), size=top_n, replace=False, p=probs)
selected_chroms = np.take(population, selected_idx, axis=0)
Step5: 다음 세대 염색체 생성 (Crossover & Mutation)
Step5는 기존 local search의 단점을 보완하기 위한 단계로 다음 세대 염색체를 생성하는 과정을 통해 search space를 넓힙니다. 해당 과정은 crossover와 mutation 두 단계에 걸쳐 진행됩니다. 먼저 crossover는 population에서 샘플링한 두 염색체의 일부를 섞어 새로운 다음 세대 염색체를 생성하는 과정입니다. 이 때, 두 부모 염색체는 fitness에 대한 확률 값을 기반으로 population에서 샘플링되며, 두 염색체의 일부를 섞는 과정은 두 부모 염색체를 crosspoint를 기준으로 자른 후 해당 부분을 무작위로 맞교환하는 방식으로 진행됩니다. Crossover의 도식과 구현 코드는 아래와 같습니다.
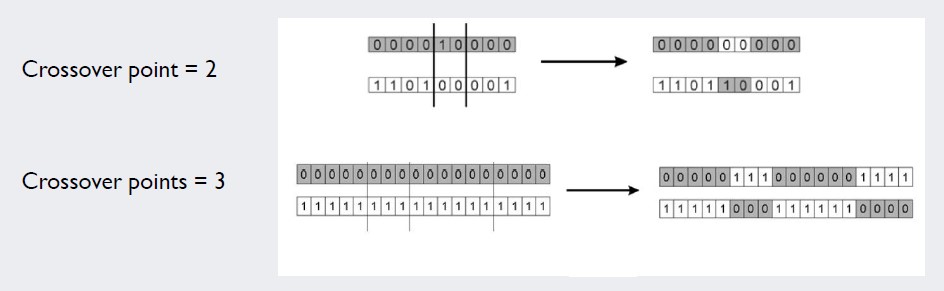Crossover
# select parants
selected_idx = np.random.choice(len(population), size=2, replace=False, p=probs)
selected_parents = np.take(population, selected_idx, axis=0)
# crossover
cross_point = np.random.choice(len(population) - 1, size=self.crossover_point, replace=False)
cross_point = [0] + list(cross_point) + [self.var_num]
cross_tf = [t >= 0.5 for t in np.random.uniform(0, 1, size=self.crossover_point + 1)]
child_1 = []
child_2 = []
# do cross over
for i in range(len(cross_tf)):
if cross_tf[i]:
child_1 += list(selected_parents[1])[cross_point[i]:cross_point[i + 1]]
child_2 += list(selected_parents[0])[cross_point[i]:cross_point[i + 1]]
else:
child_1 += list(selected_parents[0])[cross_point[i]:cross_point[i + 1]]
child_2 += list(selected_parents[1])[cross_point[i]:cross_point[i + 1]]
다음으로 mutation은 이름대로 돌연변이를 생성함으로써 search space를 넓히고 국소 최적해를 피할 가능성을 높이는 방법입니다. mutation은 crossover를 통해 생성된 자식 염색체들의 집합을 대상으로 진행됩니다. 각각의 자식 염색체에 대해 해당 염색체에 존재하는 유전자를 mutation 비율만큼 무작위로 반대 값으로 변형하는 방법입니다. 즉, mutation된 유전자는 원래 값이 1이었으면 0으로, 0이었으면 1로 대체됩니다. 해당 코드는 아래와 같습니다.
Mutation
# generate mutents
mutents = np.random.choice([True, False], size=[len(children), self.var_num], p=[mutate_ratio, 1 - mutate_ratio])
# change mutents
for i in range(mutents.shape[0]):
for j in range(mutents.shape[1]):
if mutents[i,j] == True:
children[i][j] = 1 - children[i][j]
Step6: 최종 변수 집합 선택
위에서 소개한 유전 알고리즘의 step2~step5 총 4단계를 반복해 변수 선택을 진행합니다. 앞의 진행과정에서 step1에서 설정한 stopping criteria를 만족하면 유전 알고리즘을 종료하고 우수 염색체 최종 선택합니다. 해당 단계에서 최종적으로 선택된 염색체에서 유전자가 1에 해당하는 변수들의 집합이 최종 변수 집합이 됩니다.
이번 포스팅에서는 지도 차원 축소 방법 중 Forward Selection, Backward Elimination, Stepwise Selection, 그리고 Genetic Algorithm에 대해 살펴보았습니다. 위의 본문에서는 각 방법의 설명과 중요 구현 코드를 중점적으로 소개했습니다. 아래의 전체 구현 코드를 첨부합니다. 긴 글 읽어주셔서 감사합니다.
import numpy as np
import pandas as pd
from scipy import stats
class Variable_Selection():
def __init__(self, model, X, y, eval_metric, feature_names):
'''
model: model to fit
X: input data
y: target data
eval_metric: metrics for evaluation, 'AIC' or 'adj_R_sq' should be used
feature_names: the list of variable names in input data
'''
self.model = model
self.X = X
self.y = y
self.eval_metric = eval_metric
self.feature_names = feature_names
self.n = np.shape(X)[0]
self.var_num = np.shape(X)[1]
self.all_vars = list(np.arange(self.var_num))
def metric(self, used_vars):
used_X = np.take(self.X, used_vars, axis=1)
fitted_model = self.model.fit(used_X, self.y)
y_pred = fitted_model.predict(used_X)
SSE = np.sum((self.y - y_pred) ** 2)
SST = np.sum((self.y - np.mean(self.y)) ** 2)
AIC = self.n * np.log(SSE / self.n) + 2 * len(used_vars)
adj_R_sq = 1 - (self.n - 1) / (self.n - (len(used_vars) + 1)) * SSE / SST
return {"AIC": AIC, "adj_R_sq": adj_R_sq}, fitted_model
def p_value(self, fitted_model, used_vars):
used_X = np.take(self.X, used_vars, axis=1)
params = np.append(fitted_model.intercept_, fitted_model.coef_)
y_pred = fitted_model.predict(used_X)
const_X = pd.DataFrame({"Constant": np.ones(len(used_X))}).join(pd.DataFrame(used_X))
MSE = (sum((self.y - y_pred) ** 2)) / (len(const_X) - len(const_X.columns))
var_b = MSE * (np.linalg.inv(np.dot(const_X.T, const_X)).diagonal())
sd_b = np.sqrt(var_b)
ts_b = params / sd_b
pvalue = [2 * (1 - stats.t.cdf(np.abs(i), (len(const_X) - 1))) for i in ts_b]
return pvalue[1:]
def forward_cell(self, selected_vars):
candidate_vars = list(set(self.all_vars) - set(selected_vars))
candidate_vars_crt, pvalues = [], []
for i in range(len(candidate_vars)):
used_vars = selected_vars + [candidate_vars[i]]
candidate_var_crt, fitted_model = self.metric(used_vars)
candidate_vars_crt.append(candidate_var_crt[self.eval_metric])
pvalue = self.p_value(fitted_model, used_vars)
pvalues.append(pvalue)
if self.eval_metric == 'AIC':
selected_idx = np.argmin(candidate_vars_crt)
elif self.eval_metric == 'adj_R_sq':
selected_idx = np.argmax(candidate_vars_crt)
selected_var = candidate_vars[selected_idx]
selected_pvalue = pvalues[selected_idx][-1]
return selected_var, selected_pvalue
def forward_selection(self, alpha):
selected_vars = []
for _ in range(self.var_num):
selected_var, selected_pvalue = self.forward_cell(selected_vars)
if selected_pvalue <= alpha:
selected_vars.append(selected_var)
else:
break
return self.feature_names[selected_vars]
def backward_cell(self, selected_vars):
used_X = np.take(self.X, selected_vars, axis=1)
fitted_model = self.model.fit(used_X, self.y)
pvalues = self.p_value(fitted_model, selected_vars)
candidate_vars = selected_vars
candidate_vars_crt = []
for i in range(len(candidate_vars)):
used_vars = candidate_vars[:i] + candidate_vars[i + 1:]
candidate_var_crt, fitted_model = self.metric(used_vars)
candidate_vars_crt.append(candidate_var_crt[self.eval_metric])
if self.eval_metric == 'AIC':
eliminated_idx = np.argmin(candidate_vars_crt)
elif self.eval_metric == 'adj_R_sq':
eliminated_idx = np.argmax(candidate_vars_crt)
eliminated_var = candidate_vars[eliminated_idx]
eliminated_pvalue = pvalues[selected_vars.index(eliminated_var)]
return eliminated_var, eliminated_pvalue
def backward_selection(self, alpha):
selected_vars = self.all_vars
for _ in range(self.var_num):
eliminated_var, eliminated_pvalue = self.backward_cell( selected_vars)
if eliminated_pvalue >= alpha:
selected_vars.remove(eliminated_var)
else:
break
return self.feature_names[selected_vars]
def stepwise_selection(self, alpha):
selected_vars = []
i = 0
while len(selected_vars) <= self.var_num:
if i == 0:
# do forward selection
selected_var, selected_pvalue = self.forward_cell(selected_vars)
if selected_pvalue <= alpha:
selected_vars.append(selected_var)
else:
# backup for comparision
before_selected_vars = np.copy(selected_vars).tolist()
# do forward selection
selected_var, selected_pvalue = self.forward_cell(selected_vars)
if selected_pvalue <= alpha:
selected_vars.append(selected_var)
# do backward selection
eliminated_var, eliminated_pvalue = self.backward_cell(selected_vars)
if eliminated_pvalue >= alpha:
selected_vars.remove(eliminated_var)
## Stopping criteria
if before_selected_vars == selected_vars:
break
i += 1
return self.feature_names[selected_vars]
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
boston = load_boston()
X = boston.data
y = boston.target
var_names = boston.feature_names
model = LinearRegression(fit_intercept=True)
VS = Variable_Selection(model, X, y, 'AIC', var_names)
VS.forward_selection(0.1)
# result: ['LSTAT', 'RM', 'PTRATIO', 'DIS', 'NOX', 'CHAS', 'B', 'ZN', 'CRIM', 'RAD', 'TAX']
VS.backward_selection(0.1)
# result: ['CRIM', 'ZN', 'CHAS', 'NOX', 'RM', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT']
VS.stepwise_selection(0.1)
# result: ['LSTAT', 'RM', 'PTRATIO', 'DIS', 'NOX', 'CHAS', 'B', 'ZN', 'CRIM', 'RAD', 'TAX']
import numpy as np
class Genetic_Algorithm:
def __init__(self, model, X, y, pop_size, eval_metric, crossover_point, chrom_ratio=0.5, top_ratio=0.2):
'''
model: model to fit
X: input data
y: target data
pop_size: the number of chromosomes (population size)
eval_metric: metrics for evaluation, 'AIC' or 'adj_R_sq' should be used
crossover_point: the number of crossover point
chrom_ratio: probability of chroms to be 1
top_ratio: the ratio of parents that will transfer to next population
'''
self.model = model
self.X = X
self.y = y
self.pop_size = pop_size
self.eval_metric = eval_metric
self.crossover_point = crossover_point
self.chrom_ratio = chrom_ratio
self.top_ratio = top_ratio
self.n = np.shape(X)[0]
self.var_num = np.shape(X)[1]
def metric(self, used_vars):
used_X = np.take(self.X, used_vars, axis=1)
fitted_model = self.model.fit(used_X, self.y)
y_pred = fitted_model.predict(used_X)
SSE = np.sum((self.y - y_pred) ** 2)
SST = np.sum((self.y - np.mean(self.y)) ** 2)
AIC = self.n * np.log(SSE / self.n) + 2 * len(used_vars)
adj_R_sq = 1 - (self.n - 1) / (self.n - (len(used_vars) + 1)) * SSE / SST
return {"AIC": AIC, "adj_R_sq": adj_R_sq}
def fitness_eval(self, population):
fitness_values = []
for chrom in population:
# error message when 0 variable selected
if sum(chrom) == 0:
raise ValueError('0 variables selected')
selected_vars = [c for c, v in zip(range(self.var_num), chrom) if v == 1]
fitness = self.metric(selected_vars)[self.eval_metric]
fitness_values.append(fitness)
return fitness_values
def selection(self, population, fitness_values):
probs = fitness_values / sum(fitness_values)
top_n = int(self.pop_size * self.top_ratio)
selected_idx = np.random.choice(len(population), size=top_n, replace=False, p=probs)
selected_chroms = np.take(population, selected_idx, axis=0)
return selected_chroms
def crossover(self, population, fitness_values):
probs = fitness_values / sum(fitness_values)
crossover_num = int((self.pop_size * (1-self.top_ratio)) / 2)
### Cross over
children = []
for i in range(crossover_num):
# select parants
selected_idx = np.random.choice(len(population), size=2, replace=False, p=probs)
selected_parents = np.take(population, selected_idx, axis=0)
# crossover
cross_point = np.random.choice(len(population) - 1, size=self.crossover_point, replace=False)
cross_point = [0] + list(cross_point) + [self.var_num]
cross_tf = [t >= 0.5 for t in np.random.uniform(0, 1, size=self.crossover_point + 1)]
child_1 = []
child_2 = []
# do cross over
for i in range(len(cross_tf)):
if cross_tf[i]:
child_1 += list(selected_parents[1])[cross_point[i]:cross_point[i + 1]]
child_2 += list(selected_parents[0])[cross_point[i]:cross_point[i + 1]]
else:
child_1 += list(selected_parents[0])[cross_point[i]:cross_point[i + 1]]
child_2 += list(selected_parents[1])[cross_point[i]:cross_point[i + 1]]
children.append(child_1)
children.append(child_2)
return children
def mutate(self, children, mutate_ratio):
# generate mutents
mutents = np.random.choice([True, False], size=[len(children), self.var_num], p=[mutate_ratio, 1 - mutate_ratio])
# change mutents
for i in range(mutents.shape[0]):
for j in range(mutents.shape[1]):
if mutents[i,j] == True:
children[i][j] = 1 - children[i][j]
return children
def GA(self, feature_names, max_iter, mutate_ratio=0.01):
# Initialize
population = []
for i in range(self.pop_size):
# generate one chrom
chrom = np.random.choice([0, 1], size=(self.var_num), p=[1-self.chrom_ratio, self.chrom_ratio])
population.append(chrom)
# Iteration loop
for i in range(max_iter):
# Fitness evaluation
fitness_values = self.fitness_eval(population)
# Selection
selected_chroms = self.selection(population, fitness_values)
# Cross over
crossover_children = self.crossover(population, fitness_values)
# Mutate
mutate_children = self.mutate(crossover_children, mutate_ratio)
# Merge top 2 and final variable set
next_population = list(selected_chroms) + mutate_children
if i % 10 == 0:
print("Finished %dth generation !!" % i)
# Final evaluation
final_fitness_values = self.fitness_eval(next_population)
final_selected_idx = np.argmax(final_fitness_values)
final_selected_var_idx = [c for c, v in zip(range(self.pop_size), next_population[final_selected_idx]) if v == 1]
final_selected_var = feature_names[final_selected_var_idx]
return final_selected_var
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
boston = load_boston()
X = boston.data
y = boston.target
model = LinearRegression(fit_intercept=True)
GA = Genetic_Algorithm(model, X, y, pop_size=10, eval_metric='AIC', crossover_point=2, chrom_ratio=0.7, top_ratio=0.2)
GA.GA(boston.feature_names, max_iter=100)
# result: ['CRIM', 'INDUS', 'CHAS', 'NOX', 'AGE', 'DIS', 'RAD', 'TAX']
